當使用振動數據時，特別是與建模系統結合使用時，測量數據通常需要作為加速度，速度和位移。有時，不同的分析組需要以不同的形式測量信號。顯然，即使我們能夠同時測量所有三個也是不切實際的。從物理上講，將三種不同類型的傳感器放在同一個地方幾乎是不可能的。

加速度計有各種類型和尺寸，有很多選擇。有些類型可以測量到DC（0Hz），其他類型可以測量***沖擊負載等等。

真正的測速儀是非常罕見的，但他們確實存在。基于線圈和磁體方案的一個有趣的類是自供電的。

直接位移測量并不罕見。有些使用應變計，但許多其他人使用電容效應或感應射頻機制直接測量位移。電容和電感類型的優點是它們是非接觸式探針并且不會影響局部質量。

但無論如何它并不重要，因為如果我們測量加速度，速度或位移，那么通過明智地使用積分或微分來轉換它們肯定是簡單的數學，如下所示。

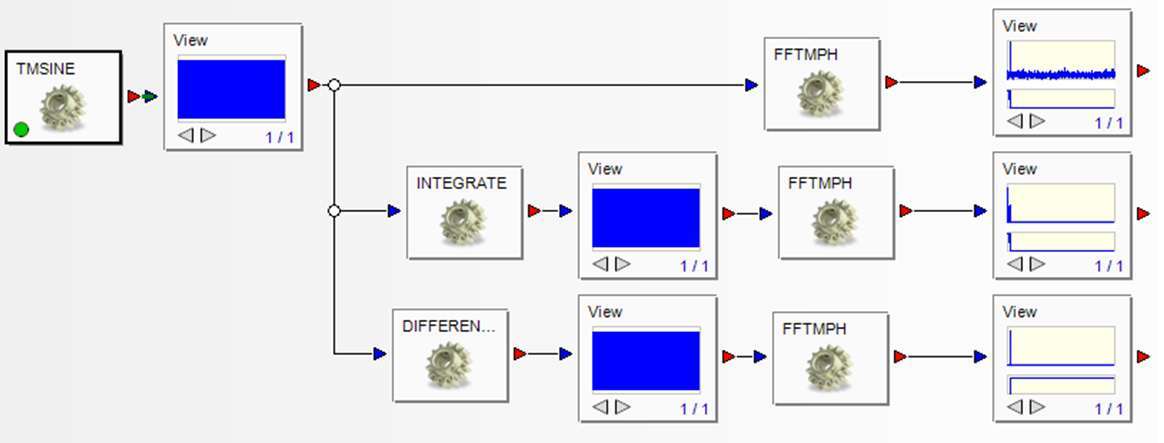
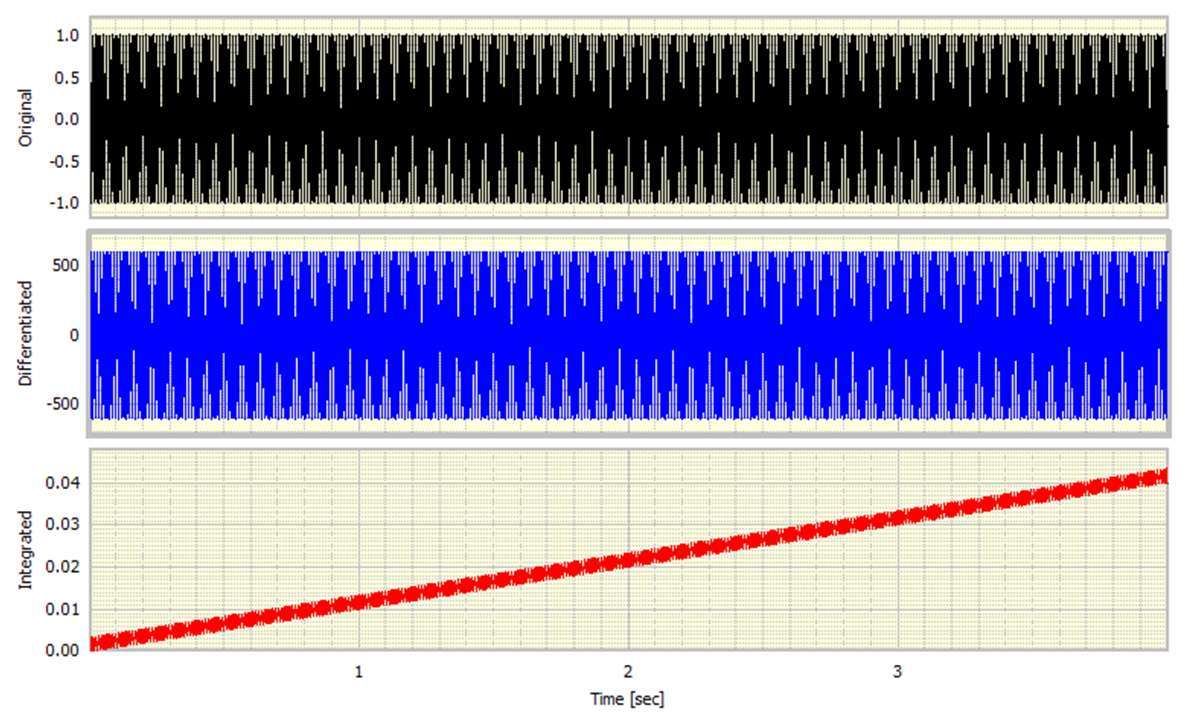
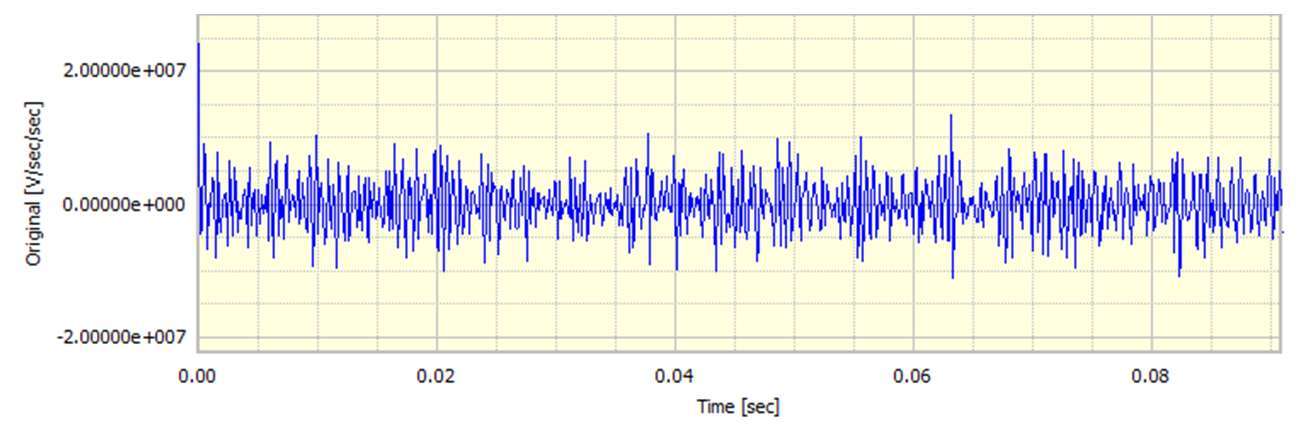
現在讓我們用經典的正弦波信號來看這個，看看區分或積分它的效果。為了避免其他副作用，該示例使用單位幅度的96Hz正弦波，以8192個樣本/秒生成32768個樣本。將這些視為時間歷史和頻率的函數是有用的。也就是說，使用DATS工作表處理原始生成的正弦波，如圖1所示。

圖1：工作表計算頻譜

看一下波形的一部分，我們得到了一個經典的結果，如圖2所示。

圖2：原始的，差異化的和綜合的時間歷史

在數學術語中，如果那么差分是，并且積分是C所謂的“積分常數”。在這兩種情況下，有90°的相移0，其接通正弦成余弦。 差值乘以。積分除以，也被否定并且已經添加了偏移，在這種情況下是合成幅度的一半，導致積分信號完全為正。例如，如果原始信號表示加速度，那么積分信號就是速度，顯然我們不希望它完全是正的。該積分常數是標準積分方法的假象。

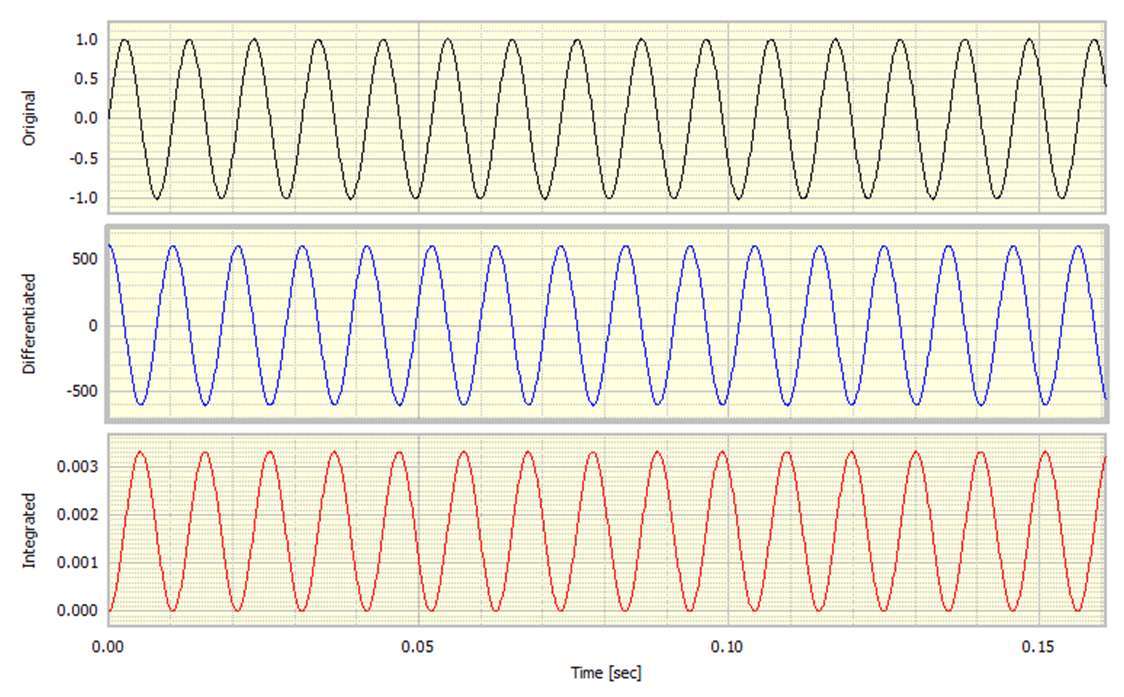
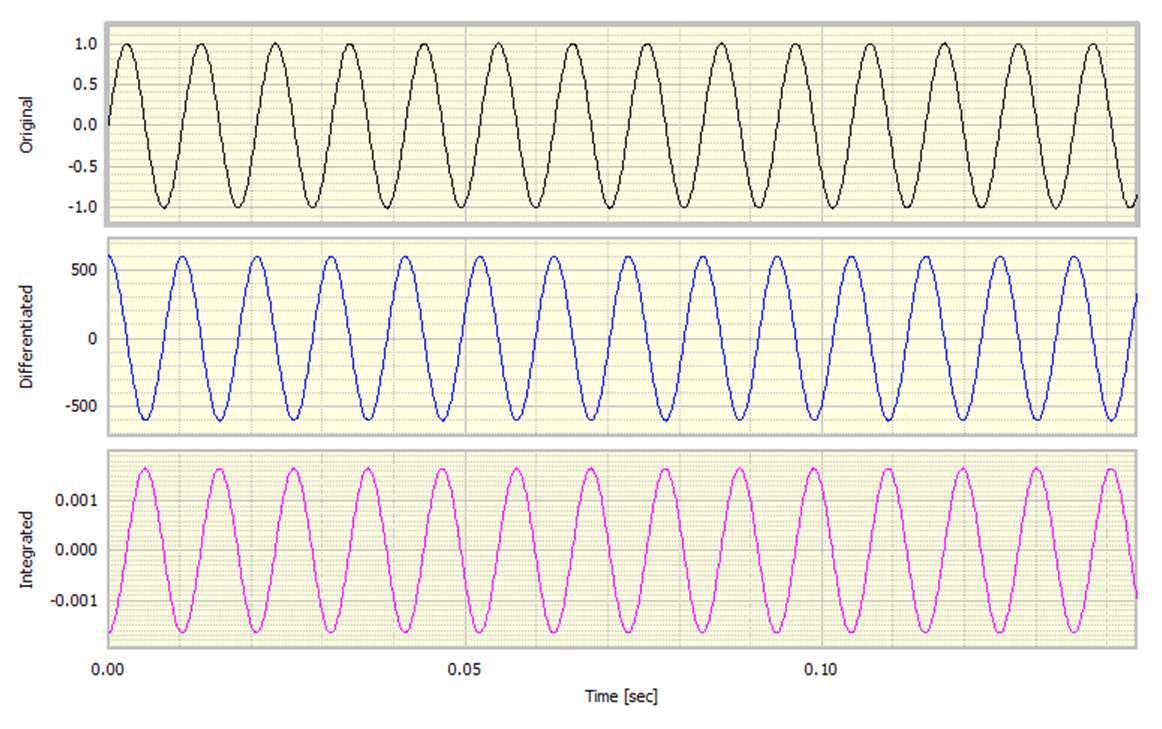
對于數學傾向，它是執行通常被稱為不定積分的結果。解決方案非常簡單。在進行基于標準時間的積分之后，我們應該自動將結果減小到具有零均值。也就是說，我們確保沒有殘余的DC偏移。計算過程被修改為包括該動作，結果如圖3所示。注意積分信號如何正如我們所期望的那樣是正面的和負面的。

圖3：調整為零均值

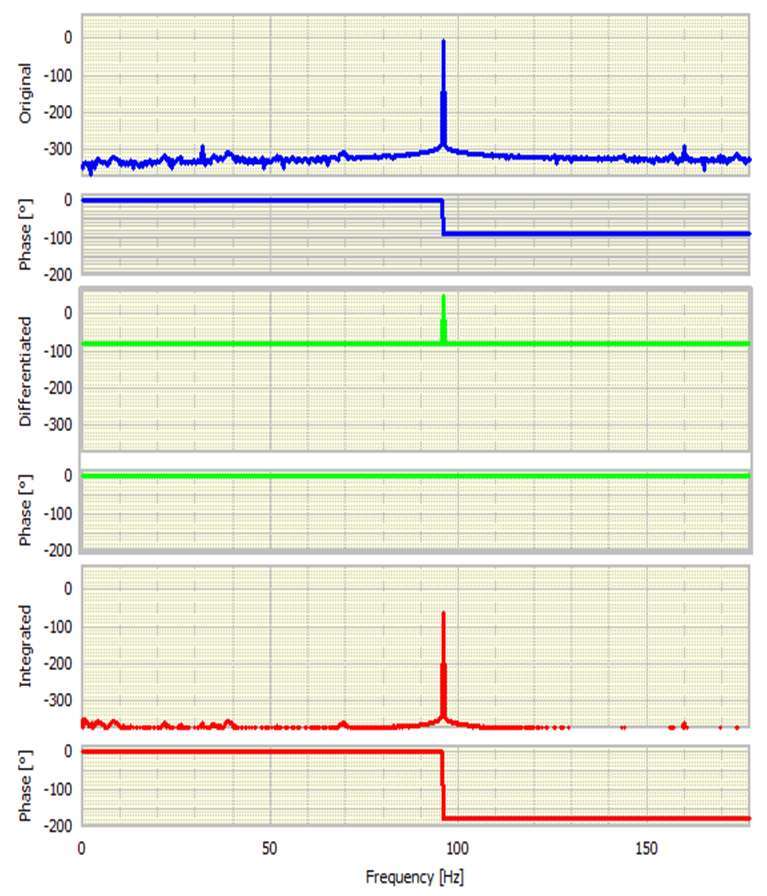
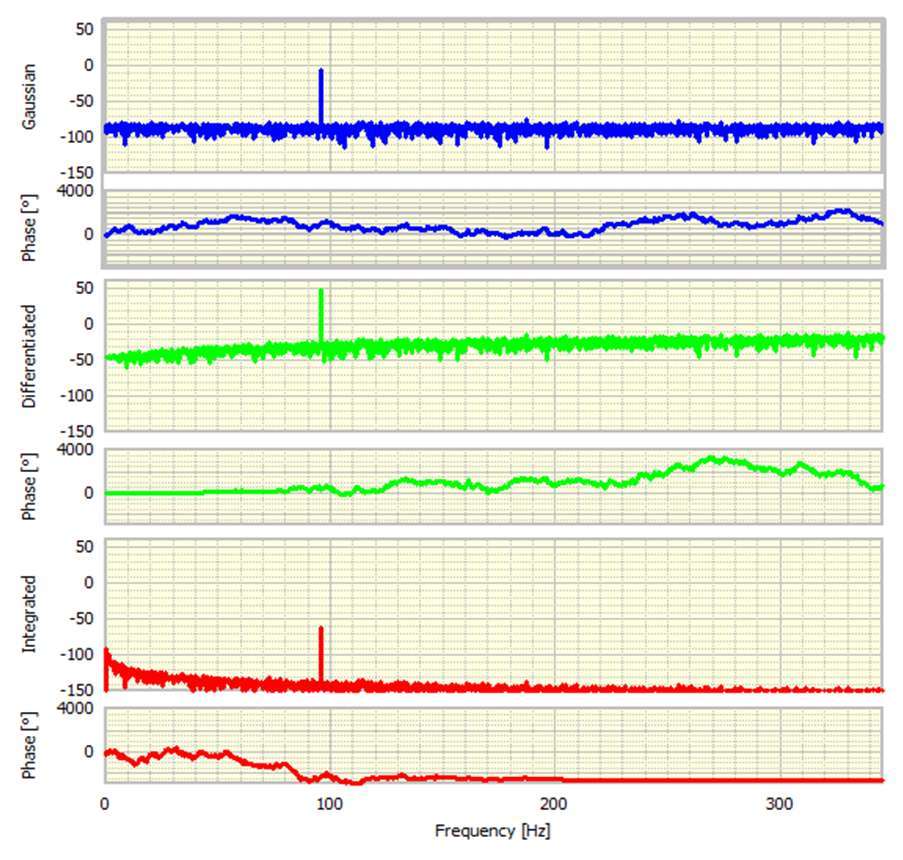
查看三個信號的傅立葉變換也很有趣。這些在圖4中以模量（振幅）和相位形式示出。模數以dB表示，相位以度為單位。

圖4：傅立葉變換

***先看相位，原始正弦波的相移為-90 0。這完全符合預期，因為FFT的基礎實際上是余弦。差分信號的相位變化為零，因為它現在是純余弦。積分信號具有180度相位變化，表示它是負余弦。

原始信號的動態范圍遠遠超過300 dB，這并不奇怪，因為它是在雙精度軟件中生成的。這相當于50位精度ADC！集成信號顯示出類似的動態范圍，但***初看起來令人驚訝的是，差分信號已經失去了動態范圍的一半。我們稍后會回到這一點。

在許多數據采集系統中，小DC偏移并不罕見。有些提供交流耦合（***通濾波）以***小化任何偏移。這會如何影響合成信號？為了說明這一點，將0.01（幅度的1％）的小DC偏移添加到原始正弦波信號中，結果如下所示。

圖5：與小DC偏移積分的結果

對原件的影響基本上不明顯。類似地，差分信號如預期的那樣不變。但是對集成信號的影響是非常顯著的。小的DC偏移產生了巨大的趨勢。我們在4秒內積累了0.01常數，累積的“漂移”為0.04。潛在的集成信號仍然很明顯，并疊加在這個漂移上。

我們如何避免這種情況？只需將輸入減少為零均值，通常稱為正規化。

注意，在這個時刻，當我們進行微分時，我們不必對初始信號做任何事情，但是我們必須在積分之前去除任何DC偏移以防止“漂移”并且還從集成信號中去除DC偏移消除整合的常數。因此，在這個階段，人們可能會試圖得出結論，使用差異化方案可能是***好的前進方式。但是，當我們添加噪音時情況會發生變化。

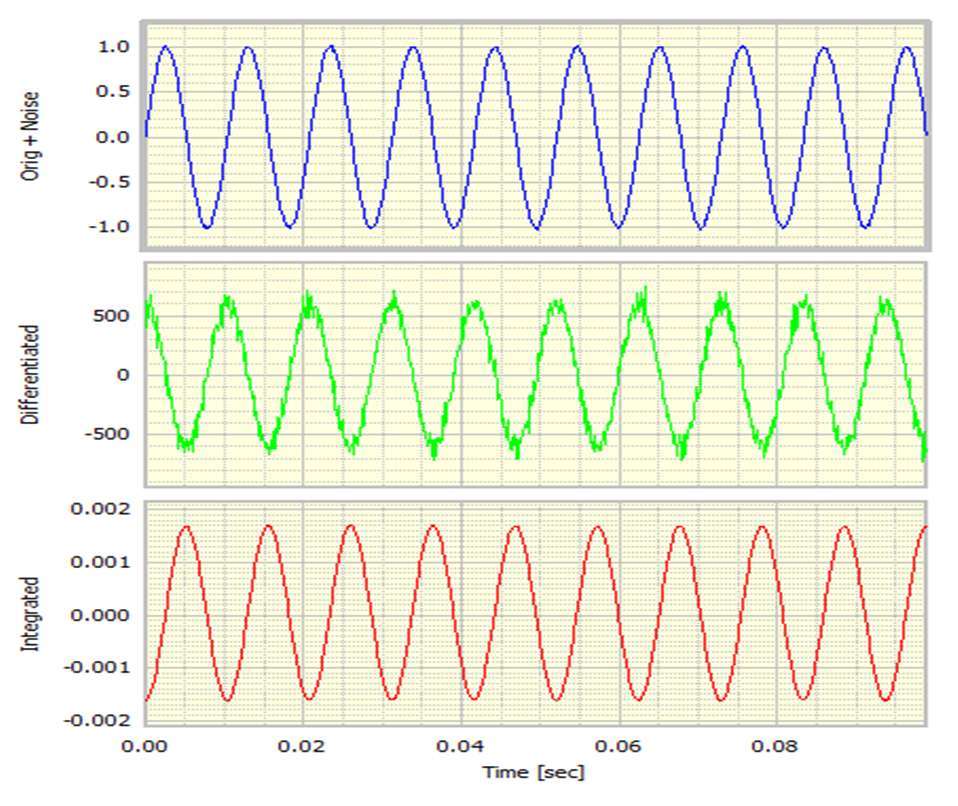
***先，在原始正弦波上添加了一個小的隨機噪聲信號。

圖6：添加少量噪音

原始信號上的眼睛無法辨別噪聲，但差分信號變得非常嘈雜。集成信號保持平滑。然而，我們可以很好地識別主導頻率。

圖7：噪聲信號的光譜

如果檢查噪聲信號的相位，可以看到它現在到處都是，并且基本上不再有任何值。使用自動相位展開，如果相位已經在360 °范圍內顯示，則它將完全填充相位圖區域。

具有附加噪聲的原始信號的動態范圍約為90dB，差分和積分信號具有相似的范圍。也就是說，增加的噪音主導了范圍。

要注意的另一個方面是集成信號上的噪聲的背景電平在較低頻率上升。這被稱為1 / f噪聲（一個超過f噪聲）。這設定了有效的較低頻率限制，低于該頻率限制，集成不再可行。

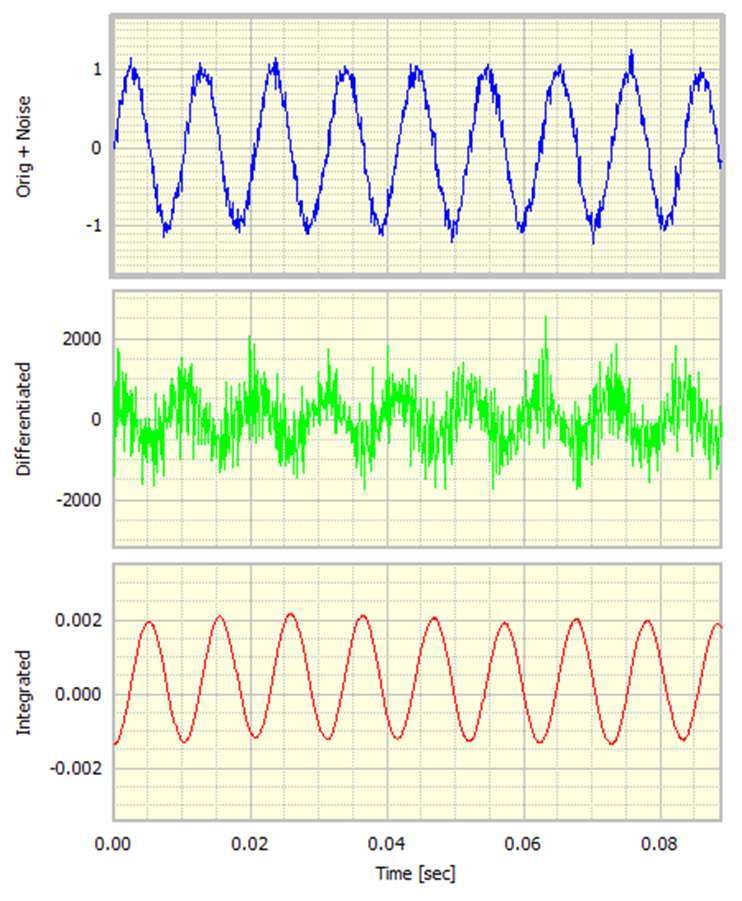
為了強調噪聲的挑戰，下一個例子具有非常大的噪聲含量。

圖8：添加了更多噪聲的時間序列

這里原始信號的噪聲很明顯。差分信號實際上是無用的，但集成信號相對干凈。為了說明這一點，嘈雜的正弦波被區分了兩次。結果如下所示。原始正弦波的所有痕跡似乎已經消失，或者更確切地說，已經在噪音中消失了。

圖9：噪聲信號分化兩次

結論現在很清楚。如果沒有特殊情況，那么經驗表明***好用加速度計測量振動。但是，如果需要對速度或位移進行任何積分，則需要注意去除極低頻率。

***后一點，為什么差異化要比整合更吵？答案是差異是一個減法過程，在它的基本水平上，我們取兩個連續值之間的差異，然后除以樣本之間的時間。兩個相鄰的數據點的大小通常非常相似。因此，差異很小并且準確性會降低，然后我們除以通常是小的時間差，這往往會放大任何錯誤。在水獺手上整合是另外的。由于任何寬帶噪聲往往是連續的，不同的符號，然后噪聲抵消。

當然，這篇文章并不能說明整個故事，但它提供了一個非常簡單的良好實踐指南。